【Dart】vector_mathで作るレイトレーシング 1

本連載について
vector_math
プロジェクトの準備
カメラ行列
1. makeViewMatrix
2. makePerspectiveMatrix
光線の生成
球との交差判定
交差判定画像の生成
まとめ

本連載について

最近ではGPUを使用したリアルタイムレイトレーシングがゲームなどでも行われていますが、レイトレーシングを行うプログラムを自分で作ってみるというのも面白いのではないかと思い、この連載を書き始めました。

現時点での本連載のイメージを書いておきます。（続ける中で変わるかもしれません）

ある程度一通り動くレイトレーシングを実装することが目標
- レイトレーシングの仕組みがおおまかに理解できるレベル
- 数学的な説明は控え目
- 本格的な高速化手法などには触れない
最初はDartのコマンドラインで実装
必要に応じて途中からFlutterに移行
vector_mathを使用

最後にvector_mathという言葉が出ましたが、vector_mathの存在が本連載を行おうと思ったきっかけの1つです。まずは、vector_mathについて説明していきたいと思います。

vector_math

DartやFlutterで使用できる線形代数ライブラリとしてGoogleが開発しているのがvector_mathです。ベクトルや行列について実装されているのはもちろんのこと、カメラや球、三角形などについても扱うことができるようになっています。また、Rayのような光線を扱うためのクラスまで用意されています。このことからvector_mathを使用すればレイトレーシングが簡単に実装できるのでは、と考えました。本連載で使用することになるクラスを紹介していきます。

Vector3

ベクトルを扱うクラスは次元により分かれていますが、本連載では主に3次元ベクトルであるVector3を使用する予定です。数値を指定して生成する場合はVector3コンストラクタを使用し、0初期化する場合はVector3.zero()を使用します。また、ノルムが1となるように正規化する場合はnormalize関数を使用します。だいたいこのあたりを使用することになります。

Ray

Rayは3次元ベクトルを2つ組み合わせることにより表現できる光線を表すクラスです。光線はどの位置からどの向きに向かって出ているかを情報として持っていなければいけないので、それらを2つの3次元ベクトルで表しているというわけです。

メンバとしてはoriginが光線の原点、directionが光線の向きを表します。大抵の場合はRay.originDirectionコンストラクタにより原点と向きを与えて生成します。

Matrix4

Matrix4は4×4の行列を表すクラスです。カメラの振る舞いを表したり、平行移動・回転・拡大縮小などの操作を行うために使用します。レイトレーシングに限らず3D的な表現を行う場合には肝となるところですが、vector_mathがかなりの部分を実装してくれているので、今回の連載では使い方に重点をおいて説明していく予定です。この連載の中ではMatrix4.identity()による単位行列として生成するか、後述するカメラ行列関連を生成するための関数で生成することが多いです。

Sphere

球を表すクラスです。レイトレーシングではよく球を使った画像が例として挙げられますが、Sphereクラスが用意されているので球を自作する必要はありません。この記事で後ほど触れます。

Triangle

三角形を表すクラスです。3点からなる平面を表す場合はこのTriangleを使用します。次回以降の記事で登場する予定です。

プロジェクトの準備

本連載で使用予定のクラスを確認したところで、早速実装に入っていきましょう。Dartはインストール済みであるという前提で、まずはプロジェクトを作成します。ここではraytraceというプロジェクト名で以下のようにプロジェクトを作成します。

$ dart create raytrace

これによりraytraceというディレクトリ名でプロジェクトが生成されます。この連載ではvector_mathを使用するため、以下のようにしてvector_mathが使用出来るようにします。

$ cd raytrace
$ dart pub add vector_math

これで、vector_mathが使用出来るようになりました。実行は下記のように行うことが出来ます。

$ dart run

まだソースコードを修正していないのでHello Worldが実行されるだけですが、今後もこのようにして実行していきます。また、当面はbin以下にあるraytrace.dartを修正していきます。lib以下にも同名のファイルがあるので注意してください。

なお、ここからの説明は部分的なコードを示す形が続くので、最後の方に登場する全体コードと照らし合わせながら見ていただけると幸いです。

カメラ行列

まずはカメラ行列を作り方について見ていきます。カメラ行列によってカメラの位置や向き、カメラの写り方などを表すことができます。vector_mathにはカメラ行列を作成するための関数がいくつか実装されていますが、今回は下記2つを使用します。

makeViewMatrix
makePerspectiveMatrix

makeViewMatrix

makeViewMatrixはビュー行列を作成するための関数です。ビュー行列とは、カメラの位置や向きを表す行列のことで、カメラの位置を動かしたりカメラの向きを変えたりする場合に使用します。makeViewMatrixの引数は以下の通りです。

引数の位置	型	内容
第一引数	Vector3	カメラの位置を表す3次元ベクトル
第二引数	Vector3	カメラの注視点位置を表す3次元ベクトル
第三引数	Vector3	カメラの上方向を示す3次元ベクトル

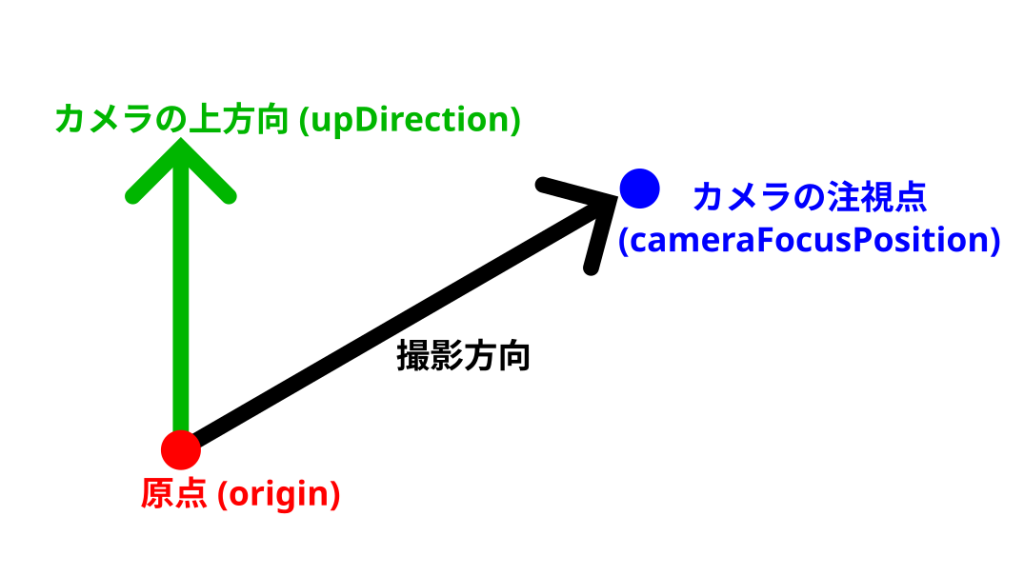
例えば、原点にあり-Z方向を向いていてY方向が上になるようなカメラのビュー行列はmakeViewMatrix関数を使用して、以下のように作成することができます。

  final viewMatrix = makeViewMatrix(
      Vector3.zero(), Vector3(0.0, 0.0, -1.0), Vector3(0.0, 1.0, 0.0));

第三引数に取るカメラの上方向を示す3次元ベクトルは第一引数と第二引数により決まるカメラの向きを表すベクトルと直交している必要はありません。例えば、第三引数をVector3(0.0, 1.0, 1.0)としても結果は単位行列のまま変わりません。第一引数と第二引数によりカメラの位置とカメラの向いている方向が決まっており、あとはカメラの向いている方向を軸とした回転の自由度しか残っていないためです。

makePerspectiveMatrix

makePerspectiveMatrixはプロジェクション行列を作成するための関数の1つです。プロジェクション行列とは、3次元の物体の座標をカメラで撮影することにより生成される2次元画像上に投影するために使用する行列です。

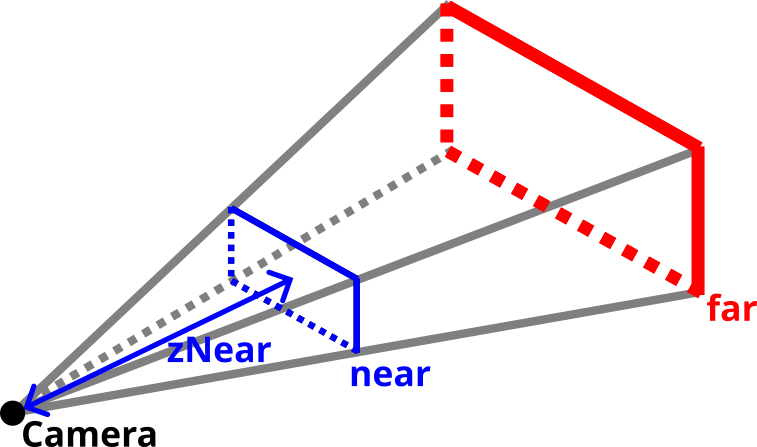
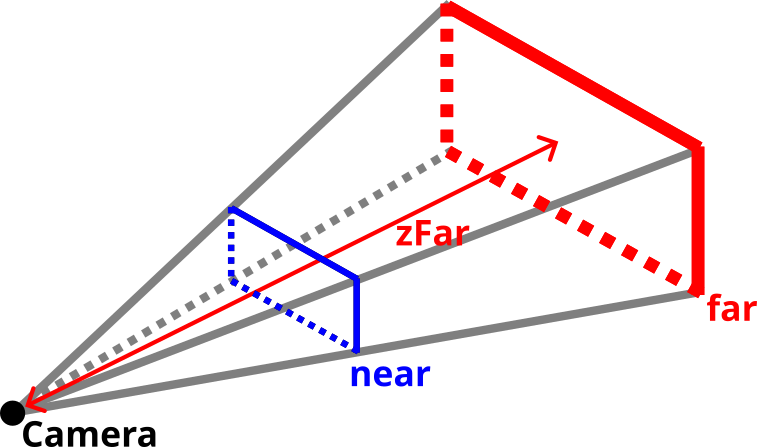
広角や望遠の具合を調節したり、撮影する画像のアスペクト比などを調節する場合に使用します。makePerspectiveMatrix関数の引数は以下の通りです。

引数の位置	型	内容
第一引数	double	カメラのY方向における視野角（ラジアン）
第二引数	double	カメラのアスペクト比
第三引数	double	カメラに写る最短距離（zNear）
第四引数	double	カメラに写る最長距離（zFar）

実際のカメラでは近すぎたり遠すぎたりすると写らないということはありませんが、CGの世界では近すぎたり遠すぎたりするものは写らないようにしています。3Dゲームなどをイメージしてもらうとよいかと思います。そのため、プロジェクション行列を作成するときにも最短距離と最長距離を指定するようになっています。CGでは上の図のnearとfarの間にあるものだけが写るようになっていますが、本連載でもnearより前の物体やfarより遠い物体は描画しないようにしていきます。

光線の生成

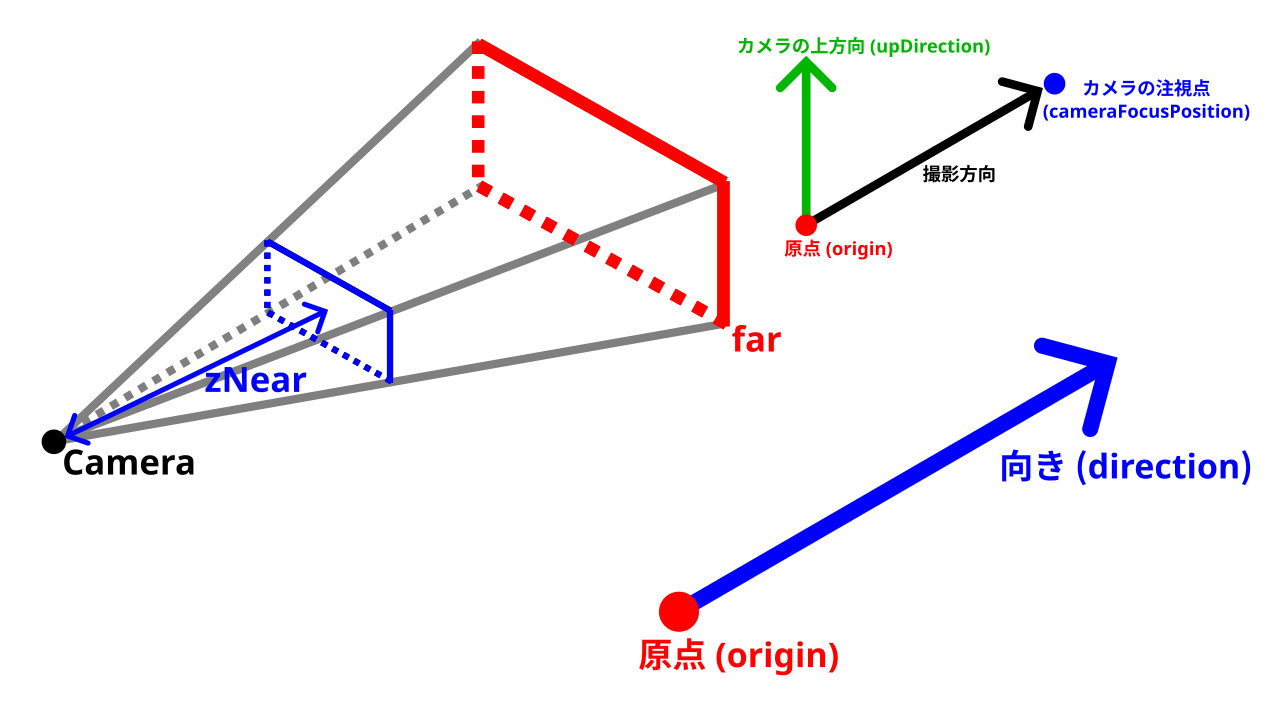
レイトレーシングの方法はいくつかありますが、本連載ではカメラから逆方向に光線を飛ばし、物体による反射を考慮して最終的に光源に到達したら光源色や反射した物体のマテリアルを考慮して画像に色をつけるという方法を取っていきます。そのため、カメラ行列から光線（逆方向）を生成する必要があるのですが、そのための関数もvector_mathにpickRay関数として用意されています。pickRay関数は以下の引数を取ります。

引数の位置	型	内容	in / out
第一引数	Matrix4	カメラ行列（プロジェクション×ビュー）	in
第二引数	num	ビューポート始点のx座標	in
第三引数	num	ビューポートの幅	in
第四引数	num	ビューポート始点のy座標	in
第五引数	num	ビューポートの高さ	in
第六引数	num	取り出す光線のビューポート上のx座標	in
第七引数	num	取り出す光線のビューポート上のy座標	in
第八引数	Vector3	最短の光線の終点となる3次元座標	out
第九引数	Vector3	最長の光線の終点となる3次元座標	out

4列目に示しているように、第八引数と第九引数はpickRay関数からの出力となります。最短、最長というのは前節のnear、farに相当します。ビューポートは作成する二次元画像と捉えてください。また、光線が取り出せたかどうかをboolで返します。カメラ行列を一旦mとしておくと、ビューポートのサイズが100×100で、そのうちの(x, y)=(30, 30)における光線を取り出す場合のpickRay関数の呼び方は以下のようになります。

  var near = Vector3.zero(), far = Vector3.zero();
  pickRay(m, 0, 100, 0, 100, 30, 30, near, far);

取り出せたのは光線の終点の3次元座標だけなので、光線の原点（＝カメラ位置）と組み合わせてRayにします。

  // cameraPositionはカメラ位置
  final rayNear = Ray.originDirection(cameraPosition, near - cameraPosition),
      rayFar = Ray.originDirection(cameraPosition, far - cameraPosition);

球との交差判定

光線と球の交差判定をしてみましょう。ですが、その前に球の生成方法を確認します。球はSphereクラスにより扱うことができ、球の中心座標と半径をもとに以下のように生成出来ます。

  // 中心座標が(x, y, z)=(0.0, 0.0, -10.0)、半径1.0の球
  final sphere = Sphere.centerRadius(Vector3(0.0, 0.0, -10.0), 1.0);

では、光線と球の交差判定をしてみましょう。原点から-Z方向に飛ぶ光線と(x, y, z)=(0, 0, -10)を中心とする半径1の球の交差判定は下記のように行うことができます。

  // 交差判定
  final dis = Ray.originDirection(Vector3.zero(), Vector3(0.0, 0.0, -1.0))
 .intersectsWithSphere(Sphere.centerRadius(Vector3(0.0, 0.0, -10.0), 1.0));

この例では光線と球は交差するので、disは交差する位置での光線の長さである9.0になります。もし光線と球が交差しない場合にはdisはnullとなります。例えば、球の中心を(x, y, z)=(2, 0, -10)にずらしてみましょう。この場合はnullになります。

交差判定画像の生成

交差判定画像を作ってみます。前節では1本の光線と球の交差判定を行いましたが、画像の各ピクセルに対応する光線を生成してそれぞれで交差判定を行い、その結果をもとに画像を生成してあげれば交差判定結果を示す画像を生成できます。ここまで説明してきたことの組み合わせになるので、ここでは最初から全体のコードを示します。

import 'package:vector_math/vector_math_64.dart';
import 'dart:math';
import 'dart:typed_data';
import 'dart:io';

void main(List<String> arguments) {
  // Viewport
  int viewportWidth = 100, viewportHeight = 100;

  // Projection
  final fov = 45.0 / 180.0 * pi,
      aspectRatio = viewportWidth / viewportHeight,
      zNear = 0.1,
      zFar = 100.0;

  // View
  final cameraPosition = Vector3.zero(),
      cameraFocusPosition = Vector3(0.0, 0.0, -1.0),
      upDirection = Vector3(0.0, 1.0, 0.0);

  // CameraMatrix
  final cameraMatrix = makePerspectiveMatrix(fov, aspectRatio, zNear, zFar) *
      makeViewMatrix(cameraPosition, cameraFocusPosition, upDirection);

  // Sphere
  final sphere = Sphere.centerRadius(Vector3(0.0, 0.0, -10.0), 3.0);

  // 画像データ
  final imageData = Uint8List(viewportWidth * viewportHeight * 3);

  // 全画素で光線を生成し交差判定
  var near = Vector3.zero(), far = Vector3.zero();
  for (var i = 0; i < viewportHeight; i++) {
    for (var j = 0; j < viewportWidth; j++) {
      if (pickRay(
          cameraMatrix, 0, viewportWidth, 0, viewportHeight, j, i, near, far)) {
        final ray = Ray.originDirection(
            cameraPosition, (near - cameraPosition).normalized());
        final minDis = (near - cameraPosition).normalize(),
            maxDis = (far - cameraPosition).normalize();

        final dis = ray.intersectsWithSphere(sphere);

        if (dis != null && minDis <= dis && dis <= maxDis) {
          imageData[(i * viewportWidth + j) * 3 + 0] = 255;
          imageData[(i * viewportWidth + j) * 3 + 1] = 255;
          imageData[(i * viewportWidth + j) * 3 + 2] = 255;
        } else {
          imageData[(i * viewportWidth + j) * 3 + 0] = 0;
          imageData[(i * viewportWidth + j) * 3 + 1] = 0;
          imageData[(i * viewportWidth + j) * 3 + 2] = 0;
        }
      }
    }
  }

  writePpm('out.ppm', viewportWidth, viewportHeight, imageData);
}

void writePpm(String filename, int width, int height, Uint8List data) {
  final f = File(filename);
  f.writeAsStringSync('P6\n$width $height\n255\n');
  f.writeAsBytesSync(data, mode: FileMode.append);
}

結果の画像がout.ppmとして出力されます。PNG形式に変換した画像を下に示します。