今回の内容
前回の記事ではカメラ行列から光線を生成し、球との交差判定を行った結果の画像を生成するところまでを説明しました。今回は以下の内容について書いていきます。
- 法線
- 拡散反射
- 光源との交差判定とモンテカルロ法
法線
法線とは面に対して垂直なベクトルのことです。三角形のような平面の場合はどの点においても法線は一定です。一方、球の場合は球の中心と着目点から求まるベクトルが法線となるので、点の位置により法線は異なります。二次元的ですが、それを表したのが下の図です。
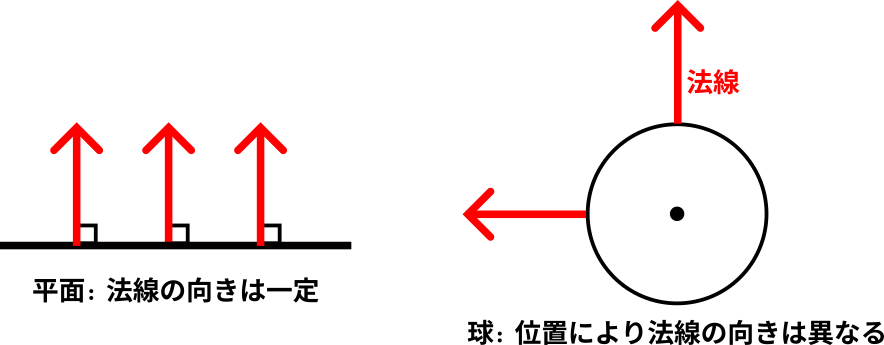
三角形を表すTriangleクラスにはcopyNormalIntoという関数が用意されており、法線を取り出すことができます。一方、Sphereクラスのには法線を取り出す関数は用意されていないので、自分で計算する必要があります。前回の最後に交差判定画像を生成しましたが、それを法線画像の生成に変えた場合のコード例は下記のようになります。
import 'package:vector_math/vector_math_64.dart';
import 'dart:math';
import 'dart:typed_data';
import 'dart:io';
void main(List<String> arguments) {
// Viewport
int viewportWidth = 100, viewportHeight = 100;
// Projection
final fov = 45.0 / 180.0 * pi,
aspectRatio = viewportWidth / viewportHeight,
zNear = 0.1,
zFar = 100.0;
// View
final cameraPosition = Vector3.zero(),
cameraFocusPosition = Vector3(0.0, 0.0, -1.0),
upDirection = Vector3(0.0, 1.0, 0.0);
// CameraMatrix
final cameraMatrix = makePerspectiveMatrix(fov, aspectRatio, zNear, zFar) *
makeViewMatrix(cameraPosition, cameraFocusPosition, upDirection);
// Sphere
final sphere = Sphere.centerRadius(Vector3(0.0, 0.0, -10.0), 3.0);
// 画像データ
final imageData = Uint8List(viewportWidth * viewportHeight * 3);
// 全画素で光線を生成し法線を計算
var near = Vector3.zero(), far = Vector3.zero();
for (var i = 0; i < viewportHeight; i++) {
for (var j = 0; j < viewportWidth; j++) {
if (pickRay(
cameraMatrix, 0, viewportWidth, 0, viewportHeight, j, i, near, far)) {
final ray = Ray.originDirection(
cameraPosition, (near - cameraPosition).normalized());
final minDis = (near - cameraPosition).normalize(),
maxDis = (far - cameraPosition).normalize();
final dis = ray.intersectsWithSphere(sphere);
if (dis != null && minDis <= dis && dis <= maxDis) {
// 法線の計算
final normal = (ray.at(dis) - sphere.center).normalized();
// 法線の各成分(-1.0~1.0)を0-255に割り当てる
imageData[(i * viewportWidth + j) * 3 + 0] =
((normal.x + 1.0) * 0.5 * 255).round();
imageData[(i * viewportWidth + j) * 3 + 1] =
((normal.y + 1.0) * 0.5 * 255).round();
imageData[(i * viewportWidth + j) * 3 + 2] =
((normal.z + 1.0) * 0.5 * 255).round();
} else {
imageData[(i * viewportWidth + j) * 3 + 0] = 0;
imageData[(i * viewportWidth + j) * 3 + 1] = 0;
imageData[(i * viewportWidth + j) * 3 + 2] = 0;
}
}
}
}
writePpm('out.ppm', viewportWidth, viewportHeight, imageData);
}
void writePpm(String filename, int width, int height, Uint8List data) {
final f = File(filename);
f.writeAsStringSync('P6\n$width $height\n255\n');
f.writeAsBytesSync(data, mode: FileMode.append);
}法線の計算は46行目で行っています。法線の各成分は-1.0~1.0の値を取るので、それを49~54行目で画素値として取りうる0~255に変換しています。実行するとout.ppmとしてPPM画像が出力されます。下にPNGに変換したものを示します。

画素値のRGBそれぞれがx方向、y方向、z方向に対応しています。この例ではカメラが原点にあり-Z方向を向いておりY方向が上となっているので、赤色であるほど法線は右を向いていて、緑色であるほど法線は上を向いていて、青色であるほど法線はカメラ側を向いているということになります。
拡散反射
レイトレーシングは反射や屈折といった物理現象をシミュレートする必要があります。反射にはいくつかの種類がありますが、まず最初に拡散反射について見ていきます。拡散反射以外については次回以降に触れていきたいと思います。
ざっくり書くと、拡散反射とは物体表面で様々な方向に拡散して反射する現象です。

イメージが付きにくいかもしれませんが、マットな質感をしているものは拡散反射していると言ってよいと思います。拡散反射の仕方は厳密には物体により異なりますが、拡散反射をモデル化したものとしてランバート反射というものがあります。ランバート反射は面の正規化法線ベクトルと面から光源を指す正規化ベクトルの内積に反射の強さが比例します。
例として、光源が点として存在する場合のランバート反射画像を生成してみましょう。下にコードを示します。
import 'package:vector_math/vector_math_64.dart';
import 'dart:math';
import 'dart:typed_data';
import 'dart:io';
void main(List<String> arguments) {
// Viewport
int viewportWidth = 500, viewportHeight = 500;
// Projection
final fov = 45.0 / 180.0 * pi,
aspectRatio = viewportWidth / viewportHeight,
zNear = 0.1,
zFar = 100.0;
// View
final cameraPosition = Vector3.zero(),
cameraFocusPosition = Vector3(0.0, 0.0, -1.0),
upDirection = Vector3(0.0, 1.0, 0.0);
// CameraMatrix
final cameraMatrix = makePerspectiveMatrix(fov, aspectRatio, zNear, zFar) *
makeViewMatrix(cameraPosition, cameraFocusPosition, upDirection);
// Sphere
final sphere = Sphere.centerRadius(Vector3(0.0, 0.0, -10.0), 3.0);
// Light
final lightPos = Vector3(5.0, 3.0, 0.0);
// 画像データ
final imageData = Uint8List(viewportWidth * viewportHeight * 3);
// 全画素で光線を生成し法線を計算
var near = Vector3.zero(), far = Vector3.zero();
for (var i = 0; i < viewportHeight; i++) {
for (var j = 0; j < viewportWidth; j++) {
if (pickRay(
cameraMatrix, 0, viewportWidth, 0, viewportHeight, j, i, near, far)) {
final ray = Ray.originDirection(
cameraPosition, (near - cameraPosition).normalized());
final minDis = (near - cameraPosition).normalize(),
maxDis = (far - cameraPosition).normalize();
final dis = ray.intersectsWithSphere(sphere);
if (dis != null && minDis <= dis && dis <= maxDis) {
// 交差する点
final p = ray.at(dis);
// 法線
final normal = (p - sphere.center).normalized();
// 交差する点から光源を指す単位ベクトル
final lightVec = (lightPos - p).normalized();
// 法線と交差する点から光源を指す単位ベクトルの内積をもとに画素値を決定
final val = (normal.dot(lightVec) * 255).round().clamp(0, 255);
imageData[(i * viewportWidth + j) * 3 + 0] = val;
imageData[(i * viewportWidth + j) * 3 + 1] = val;
imageData[(i * viewportWidth + j) * 3 + 2] = val;
} else {
imageData[(i * viewportWidth + j) * 3 + 0] = 0;
imageData[(i * viewportWidth + j) * 3 + 1] = 0;
imageData[(i * viewportWidth + j) * 3 + 2] = 0;
}
}
}
}
writePpm('out.ppm', viewportWidth, viewportHeight, imageData);
}
void writePpm(String filename, int width, int height, Uint8List data) {
final f = File(filename);
f.writeAsStringSync('P6\n$width $height\n255\n');
f.writeAsBytesSync(data, mode: FileMode.append);
}このコードでは画像の大きさを500×500に変更しています(8行目)。実行すると下のような画像が生成されます。

陰影が表現されていて球らしくなっています。また、光源が右上にあるので、左側から下側にかけては暗くなっています。
コードの内容について少し見ていきます。52行目で球とカメラから逆算した光線との交差点における法線を算出しています。そして、点光源は1つしかなく位置も既知なので、55行目で交差点から光源への向きを表す単位ベクトルを算出しています。ランバート反射では面の法線を表す単位ベクトルと面の位置から光源の向きを表す単位ベクトルの内積に反射の強さが比例するので、58行目でその値を求めて59~61行目で画素値として反映しています。
光源との交差判定とモンテカルロ法
前節では点光源に対してランバート反射を計算しました。ですが、実世界では光源も大きさを持っています。そこで、光源も球である場合の画像を生成してみましょう。
物体としての球が1つと光源としての球が1つある場合、球のある点がカメラからどう写るかを計算するためには下図のように光源に到達する可能性のあるあらゆる光線の経路の反射を計算する必要があります。
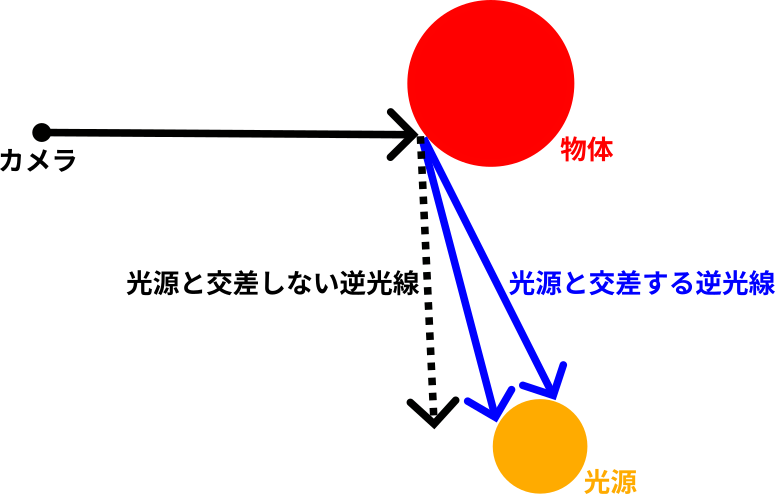
図では光源と交差する経路は2本しか示していませんが、実際には無数に存在します。今回は物体と光源が1つずつなので光源に到達する経路の範囲を特定することは可能ですが、ここでは今後のことも考えてモンテカルロ法という手法を導入することにします。モンテカルロ法は多くのサンプル数が必要なものから限られたサンプルを乱数により選択して計算する手法です。例えば、モンテカルロ法を用いて円周率の近似値を求める方法は有名かと思います。反射の計算においてもモンテカルロ法を用いるいことで正解に近い近似値を求めることができるというわけです。ここでは一旦ランバート反射のことは忘れ、球の光源がある場合の画像をモンテカルロ法を用いて生成するコード例を以下に示します。
import 'package:vector_math/vector_math_64.dart';
import 'dart:math';
import 'dart:typed_data';
import 'dart:io';
void main(List<String> arguments) {
// Viewport
int viewportWidth = 100, viewportHeight = 100;
// Projection
final fov = 45.0 / 180.0 * pi,
aspectRatio = viewportWidth / viewportHeight,
zNear = 0.1,
zFar = 100.0;
// View
final cameraPosition = Vector3.zero(),
cameraFocusPosition = Vector3(0.0, 0.0, -1.0),
upDirection = Vector3(0.0, 1.0, 0.0);
// CameraMatrix
final cameraMatrix = makePerspectiveMatrix(fov, aspectRatio, zNear, zFar) *
makeViewMatrix(cameraPosition, cameraFocusPosition, upDirection);
// Sphere
final sphere = Sphere.centerRadius(Vector3(0.0, 0.0, -10.0), 3.0);
// Light
final sphereLight = Sphere.centerRadius(Vector3(3.0, 3.0, 0.0), 1.0);
// 画像データ
final countData = List<int>.filled(viewportWidth * viewportHeight * 3, 0);
// 乱数
final rand = Random();
// 全画素で光線を生成し法線を計算
var near = Vector3.zero(), far = Vector3.zero();
for (var i = 0; i < viewportHeight; i++) {
for (var j = 0; j < viewportWidth; j++) {
if (pickRay(
cameraMatrix, 0, viewportWidth, 0, viewportHeight, j, i, near, far)) {
final ray = Ray.originDirection(
cameraPosition, (near - cameraPosition).normalized());
final minDis = (near - cameraPosition).normalize(),
maxDis = (far - cameraPosition).normalize();
final dis = ray.intersectsWithSphere(sphere);
if (dis != null && minDis <= dis && dis <= maxDis) {
// 交差する点
final p = ray.at(dis);
// 法線
final normal = (p - sphere.center).normalized();
// 法線と直交するベクトル
final nx = normal.cross(Vector3(1.0, 0.0, 0.0)),
ny = normal.cross(Vector3(0.0, 1.0, 0.0));
final n2 = ((nx.dot(nx) > ny.dot(ny)) ? nx : ny).normalized();
// サンプル数1000でモンテカルロ法を実行
for (var k = 0; k < 1000; k++) {
// 法線と直行するベクトルを法線周りにランダムに回転
Quaternion.axisAngle(normal, rand.nextDouble() * 2.0 * pi)
.rotate(n2);
// 生成した軸ベクトル周りで法線を回転
final dir =
Quaternion.axisAngle(n2, rand.nextDouble() * pi - 0.5 * pi)
.rotated(normal);
// 光線
final rayLight = Ray.originDirection(p, dir);
// 光源との交差判定
if (rayLight.intersectsWithSphere(sphereLight) != null) {
// 光源と交差したらインクリメント
countData[(i * viewportWidth + j) * 3 + 0]++;
countData[(i * viewportWidth + j) * 3 + 1]++;
countData[(i * viewportWidth + j) * 3 + 2]++;
}
}
}
}
}
}
// 0以外の画素値平均を算出
var ave = 0.0;
var n = 0;
for (final i in countData) {
if (i != 0) {
ave += i;
n++;
}
}
ave /= n;
// 0以外の画素値平均をもとに明るさを調節した画像を生成し出力
final imageData = Uint8List.fromList(countData.map((val) {
return (val / ave * 128.0).round().clamp(0, 255);
}).toList());
writePpm('out.ppm', viewportWidth, viewportHeight, imageData);
}
void writePpm(String filename, int width, int height, Uint8List data) {
final f = File(filename);
f.writeAsStringSync('P6\n$width $height\n255\n');
f.writeAsBytesSync(data, mode: FileMode.append);
}このコードを実行すると下のような画像が生成されます。

ノイズが多いですが、これはモンテカルロ法のサンプル数が少ないことによるものです。63行目の1000がサンプル数なので、これを100000にして実行してみましょう。私のPCでは45秒程度で完了しますが、下のような画像が生成されます。

このようにモンテカルロ法はサンプル数が多ければ多いほど、それらしい結果を得ることができます。
それではコードの中身を見ていきます。まず、58~60行目で法線と直交するベクトルを求めています。平面の場合は直交するベクトルは1つ(逆方向も合わせれば2つ)ですが、ベクトルに直交するベクトルは無数にあります。そのため、法線とx軸もしくは法線とy軸のなす平面に直交するベクトルを求めています。もし法線がx軸かy軸のどちらかと平行である場合、直交するベクトルが求まらないので2パターンの平面で直交するベクトルを求めるようにしています。どちらでも求まる場合はどちらを採用してもよいのですが、ここではとりあえずノルムの大きい方を採用しています(60行目)。ここで求めた法線と直交するベクトルは様々な方向の光線を生成するために使用します。
さきほども説明しましたが、63行目がモンテカルロ法のためのループ開始になります。このコード例ではサンプル数1000でモンテカルロ法を実行するため、1000回のループを回すようにしています。65~66行目ではモンテカルロ法のループ開始前に求めた法線と直交するベクトルを法線を軸としてランダムに回転しています。Quartanionとは四元数を扱うクラスであり、回転を扱うときに使用することの多いものです。Quartanion.axisAngleにより第一引数のベクトルを軸として第二引数の角度(ラジアン)だけ回転することを表す四元数を生成することが出来ます。つまり、65~66行目では法線と直交するベクトルを法線を軸として0~360度だけランダムに回転したベクトルを算出しています。
そして、69~71行目では算出したベクトルを軸として0~90度法線を回転しています。これにより、カメラから逆算した経路と球の交差点からさらに逆算した経路の向きのうちの1つをランダムに得ることが出来ます。74行目ではこれを元に光線を生成しています。
77行目では、球の光源と74行目で生成した光線との交差判定を行っています。交差する場合には79~81行目で交差した回数のカウント値をインクリメントしています。
画像の全画素についてモンテカルロ法の実施が終わった後、90~98行目でカウント値が0でない画素値のカウント平均値を求めています。カウント値をもとに画像を生成する際にどの程度のカウント値をどの程度の画素値に割り当てればよいかが分からないので、カウント値の平均をもとに適当に決めてあげようという考え方です。101~103行目で実際にカウント値を画素値に割り当てています。
まとめ
今回は以下の内容について説明しました。
- 法線
- 拡散反射
- 光源との交差判定とモンテカルロ法
次回は物体同士の相互反射について説明する予定です。


コメント